История создания пакета ScaLАРАСК и его общая организаци

Важнейшая роль в численных методах принадлежит решению задач линейной алгебры. Свое отражение это находит в том факте, что все производители высокопроизводительных вычислительных систем поставляют со своими системами оптимизированные библиотеки подпрограмм, включающие главным образом подпрограммы для решения задач линейной алгебры. Так на компьютерах фирмы SUN в состав библиотеки High Performance Library входят пакеты BLAS, LINPACK и LAPACK. Аналогичный состав имеет и библиотека Compaq Extended Math Library, устанавливаемая на компьютерах фирмы Compaq на базе процессоров Alpha. Для систем на базе архитектуры x86 компания Intel предлагает библиотеку MKL (Math Kernel Library), также состоящую, главным образом, из подпрограмм для решения различных задач линейной алгебры.

С появлением многопроцессорных систем с распределенной памятью начались работы по переносу на эти платформы библиотеки LAPACK, как наиболее полно отвечающей архитектуре современных процессоров (подпрограммы оптимизированы для эффективного использования кэш-памяти). В работе по переносу библиотеки LAPACK участвовали ведущие научные и суперкомпьютерные центры США.

Результатом этой работы было создание пакета подпрограмм ScaLAPACK (Scalable LAPACK). Проект оказался успешным, и пакет фактически стал стандартом в программном обеспечении многопроцессорных систем. В этом пакете почти полностью сохранены состав и структура пакета LAPACK и почти не изменились обращения к подпрограммам верхнего уровня. В основе успеха реализации этого проекта лежали два принципиально важных решения.

Во-первых, по аналогии с пакетом LAPACK, в котором все элементарные векторные и матричные операции выполняются с помощью высокооптимизированных подпрограмм библиотеки BLAS (Basic Linear Algebra Subprograms), при реализации ScaLAPACK была разработана параллельная версия этой библиотеки - PBLAS, что избавило от необходимости радикальным образом переписывать подпрограммы верхнего уровня.

Во-вторых, все коммуникационные операции выполняются с исполь┐зованием подпрограмм из специально разработанной библиотеки BLACS (Basic Linear Algebra Communication Subprograms), в которой скрыты детали организации коммуникационной среды вычислительной системы и поэтому перенос пакета на различные многопроцессорные платформы требует настройки только этой библиотеки.

Структура пакета ScaLАРАСК

Общая структура пакета ScaLAPACK представлена на Рис. 1

Рис. 1. Структура пакета ScaLAPACK

На этом рисунке компоненты пакета, расположенные выше разделительной линии, содержат подпрограммы, которые выполняются параллельно на некотором наборе процессоров и в качестве аргументов используют векторы и матрицы, распределенные по этим процессорам. Подпрограммы из компонентов пакета, расположенные ниже разделительной линии вызываются на одном процессоре и работают с локальными данными. Каждый из компонентов пакета - это независимая библиотека подпрограмм, которая не является частью библиотеки ScaLAPACK, но необходима для ее работы. В тех случаях, когда на компьютере имеются оптимизированные фирменные реализации каких-то из этих библиотек (BLAS, LAPACK), то настоятельно рекомендуется для достижения более высокой производительности использовать именно эти реализации.

Собственно сама библиотека ScaLAPACK состоит из примерно 530 подпрограмм, которые для каждого из 4-х типов данных (вещественного, вещественного с двойной точностью, комплексного, комплексного с двойной точностью) разделяются на три категории:

• Драйверные подпрограммы, каждая из которых решает некоторую законченную задачу, например, решение системы линейных алгебраических уравнений или нахождение собственных значений вещественной симметричной матрицы. Таких подпрограмм 14 для каждого типа данных. Эти подпрограммы обращаются к вычислительным подпрограммам.
• Вычислительные подпрограммы выполняют отдельные подзадачи, например, LU-разложение матрицы или приведение вещественной симметричной матрицы к трехдиагональному виду. Набор вычислительных подпрограмм значительно перекрывает функциональные потребности драйверных подпрограмм и может использоваться самостоятельно.
• Служебные подпрограммы выполняют некоторые внутренние вспомогательные действия и, как правило, самостоятельно не используются, а вызываются из вычислительных подпрограмм.

Имена всех драйверных и вычислительных подпрограмм совпадают с именами соответствующих подпрограмм из пакета LAPACK, с той лишь разницей, что в начале имени добавляется символ P, указывающий на то, что это параллельная версия подпрограммы. Соответственно, принцип формирования имен подпрограмм имеет ту же самую схему, что и в LAPACK. Согласно этой схеме имена подпрограмм пакета имеют вид PTXXYYY, где:

Т - тип исходных данных, который может иметь следующие значения:

S - вещественный одинарной точности,

D - вещественный двойной точности,

С - комплексный одинарной точности,

Z - комплексный двойной точности;

XX - указывает вид матрицы:

DB - ленточные общего вида с преобладающими диагональными элементами,

DT - трехдиагональные общего вида с преобладающими диагональными элементами,

GB - ленточные общего вида,

GE - общего вида,

GT - трехдиагональные общего вида,

HE - эрмитовы,

PB - ленточные симметричные или эрмитовы положительно определенные,

PO - симметричные или эрмитовы положительно определенные,

PT - трехдиагональные симметричные или эрмитовы положительно определенные,

ST - симметричные трехдиагональные,

SY - симметричные,

TR - треугольные,

TZ - трапециевидные,

UN - унитарные;

YYY - указывает на выполняемые данной подпрограммой действия:

TRF - факторизация матриц,

TRS - решение СЛАУ после факторизации,

CON - оценка числа обусловленности матрицы (после факторизации),

SV - решение СЛАУ,

SVX - решение СЛАУ с дополнительными исследованиями,

EV и EVX - вычисление собственных значений и собственных векторов,

GVX - решение обобщенной задачи на собственные значения,

SVD - вычисление сингулярных значений,

RFS - уточнение решения,

LS - нахождение наименьших квадратов.

Использование библиотеки ScaLAPACK

Библиотека ScaLAPACK требует, чтобы все объекты (векторы и матрицы), являющиеся параметрами подпрограмм, были предварительно распределены по процессорам. Исходные объекты классифицируются как глобальные объекты, и параметры, описывающие их, хранятся в специальном описателе объекта - дескрипторе. Дескриптор некоторого распределенного по процессорам глобального объекта представляет собой массив целого типа, в котором хранится вся необходимая информация об исходном объекте. Части этого объекта, находящиеся в памяти какого-либо процессора, и их параметры являются локальными данными.

Для того, чтобы воспользоваться драйверной или вычислительной подпрограммой из библиотеки ScaLAPACK, необходимо последовательно выполнить 4 шага:

• инициализировать сетку процессоров;
• распределить матрицы на сетку процессоров;
• вызвать вычислительную подпрограмму;
• освободить сетку процессоров.

Библиотека подпрограмм ScaLAPACK поддерживает работу с матрицами трех типов:

• заполненными (не разреженными) прямоугольными или квадратными матрицами;
• ленточными матрицами (узкими);
• заполненными матрицами, хранящимися на внешнем носителе.

Для каждого из этих типов используется различная топология сетки процессоров и различная схема распределения данных по процессорам. Эти различия обуславливают использование четырех типов дескрипторов. Дескриптор - это массив целого типа, состоящий из 9 или 7 элементов в зависимости от типа дескриптора. Тип дескриптора, который используется для описания объекта, хранится в первой ячейке самого дескриптора. В таблице 5.1 приведены возможные значения типов дескрипторов.

Табл. 1. Типы дескрипторов

Тип дескриптора	Назначение
1	Заполненные матрицы общего вида
501	Ленточные и трехдиагональные матрицы
502	Матрица правых частей для уравнений с ленточными и трехдиагональными матрицами
601	Заполненные матрицы на внешних носителях

Инициализация сетки процессоров

Для объектов, которые описываются дескриптором типа 1, распределение по процессорам производится на двумерную сетку процессоров. На рис. 5.2 представлен пример двумерной сетки размера 2×3 из 6 процессоров.

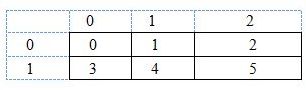
Рис. 2. Пример двумерной сетки из 6 процессоров.

При таком распределении процессоры имеют двойную нумерацию: сквозную нумерацию по всему ансамблю процессоров и координатную нумерацию по строкам и столбцам сетки. Связь между сквозной и координатной нумерациями определяется параметром процедуры при инициализации сетки (нумерация вдоль строк -

">

">

Инициализация сетки процессоров выполняется с помощью подпрограмм из библиотеки BLACS. Ниже приводится формат вызовов этих подпрограмм.

CALL BLACS_PINFO (IAM, NPROCS) - инициализирует библиотеку BLACS, устанавливает некоторый стандартный контекст для ансамбля процессоров (аналог коммуникатора в MPI), сообщает процессору его номер в ансамбле (IAM) и количество доступных задаче процессоров (NPROCS).

CALL BLACS_GET (-1, 0, ICTXT) - выполняет опрос установленного контекста (ICTXT) для использования в других подпрограммах.

CALL BLACS_GRIDINIT (ICTXT, 'Row-major', NPROW, NPCOL) - выполняет инициализацию сетки процессоров размера NPROW × NPCOL с нумерацией вдоль строк.

CALL BLACS_GRIDINFO (ICTXT, NPROW, NPCOL, MYROW, MYCOL) - сообщает процессору его позицию (MYROW, MYCOL) в сетке процессоров.

Для ленточных и трехдиагональных матриц (дескриптор 501) используется одномерная сетка процессоров (1 × NPROCS), т.е. параметр NPROW = 1, а NPCOL = NPROCS.

Для объектов, описываемых дескриптором 502 (правые части уравнений с ленточными и трехдиагональными матрицами), используется транспонированная одномерная сетка (NPROCS × 1). Работа с матрицами на внешних носителях (дескриптор 601) в данном пособии не рассматривается.

Распределение матрицы на сетку процессоров

Способ распределения матрицы на сетку процессоров также зависит от типа распределяемого объекта. Для заполненных матриц (тип дескриптора 1) принят блочно-циклический способ распределения данных по процессорам. При таком распределении матрица разбивается на блоки размера MB × NB, где MB - размер блока по строкам, а NB - размер блока по столбцам, и эти блоки циклически раскладываются по процессорам.

Проиллюстрируем это на конкретном примере распределения матрицы общего вида A(9,9), т.е. M=9, N=9, на сетке процессоров NPROW × NPCOL = 2×3 при условии, что размер блока MB × NB = 2×2.

Разбиение исходной матрицы на блоки требуемого размера будет выглядеть следующим образом (рис. 3):

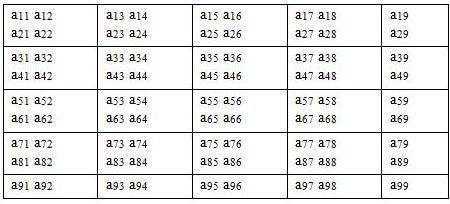
Рис. 3. Разбиение исходной матрицы 9×9 на блоки размера 2×2

После циклического распределения блоков вдоль строк и столбцов сетки процессоров получим следующее распределение матричных элементов по процессорам (рис. 4):

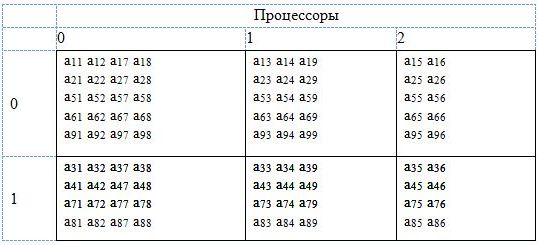
Рис. 4. Распределение элементов матрицы на сетке процессоров 2×3

Следует иметь в виду, что описанная выше процедура - это не более чем наглядная иллюстрация сути вопроса. На самом деле полная матрица A и ее разбиение на блоки (рис. 5.4) существует только в нашем воображении. В реальности наша задача состоит в том, чтобы в каждом процессоре сформировать массивы заведомо меньшей размерности, чем исходная матрица, и заполнить эти массивы матричными элементами в соответствии с принятыми параметрами распределения. Точное значение - сколько строк и столбцов должно находиться в каждом процессоре - позволяет вычислить подпрограмма-функция NUMROC из библиотеки PTOOLS, формат вызова которой приводится ниже.

">

 

NP = NUMROC (M, MB, MYROW, RSRC, NPROW)

NQ = NUMROC (N, NB, MYCOL, CSRC, NPCOL)

Здесь:

NP - число строк в локальных матрицах в строке процессоров MYROW;

NQ - число столбцов в локальных матрицах в столбце процессоров MYCOL.

Входные параметры:

M,	N	- число строк и столбцов исходной матрицы;
MB,	NB	- размеры блоков по строкам и по столбцам;
MYROW,	MYCOL	- координаты процессора в сетке процессоров;
RSRC,	CSRC	- координаты процессора, начиная с которого выполнено распределение матрицы (подразумевается возможность распределения не по всем процессорам);
NPROW,	NPCOL	- число строк и столбцов в сетке процессоров.

 

Оценить верхние значения величин NP и NQ для правильного описания размерностей локальных массивов можно с помощью формул:

NROW= (M-1)/NPROW+MB

NCOL = (N-1)/NPCOL+NB

Дескриптор для данного типа матриц - это массив целого типа из 9 элементов. Он может быть заполнен либо непосредственно с помощью операторов присваивания, либо с помощью специальной подпрограммы из библиотеки PTOOLS. Описание назначения полей дескриптора и присваиваемых им значений приводится в таблице 2.

Табл. 2. Дескриптор для заполненных матриц

DESC(1)	= 1	- тип дескриптора;
DESC(2)	= ICTXT	- контекст ансамбля процессоров;
DESC(3)	= M	- число строк исходной матрицы;
DESC(4)	= N	- число столбцов исходной матрицы;
DESC(5)	= MB	- размер блока по строкам;
DESC(6)	= NB	- размер блока по столбцам;
DESC(7)	= RSRC	- номер строки в сетке процессоров, начиная с которой распределяется матрица (обычно 0);
DESC(8)	= CSRC	- номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0);
DESC(9)	= NROW	- число строк в локальной матрице (leading dimension).

 

Вызов подпрограммы из PTOOLS, выполняющей аналогичное действие по формированию дескрипторов, имеет вид:

CALL DESCINIT(DESC, M, N, MB, NB, RSRC, CSRC, ICTXT, NROW,INFO)

Параметр INFO - статус возврата. Если INFO = 0, то подпрограмма выполнилась успешно; INFO = -I означает, что I-й параметр некорректен.

В расчетных формулах при решении задач линейной алгебры, как правило, фигурируют выражения, содержащие матричные элементы, идентифицируемые их глобальными индексами (I,J). После распределения матрицы по процессорам, а точнее, при заполнении локальных матриц на каждом процессоре, мы имеем дело с локальными индексами (i,j), поэтому очень важно знать связь между локальными и глобальными индексами. Так, если в сетке процессоров NPROW строк, а размер блока вдоль строк равен MB, то i-я строка локальных матриц в строке MYROW сетки процессоров должна быть заполнена I-ми элементами строки исходной матрицы. Формула для вычисления глобального индекса I имеет вид:

I = MYROW*MB + ((i -1)/MB)*NPROW*MB + mod(i -1,MB) + 1

Аналогично можно записать формулу для глобальных индексов столбцов:

J = MYCOL*NB + ((j -1)/NB)*NPCOL*NB + mod(j - 1,NB) + 1

Здесь деление подразумевает деление нацело, а функция mod вычисляет остаток от деления.

Симметричные и эрмитовы матрицы на сетке процессоров хранятся в виде полных матриц, однако используется при этом либо верхний, либо нижний треугольники. Поэтому в процедурах, работающих с такими матрицами, указывается параметр UPLO = 'U' для верхнего треугольника или UPLO = 'L' для нижнего треугольника.

Совершенно другой принцип распределения по процессорам принят для ленточных и трехдиагональных матриц. В этом случае используется блочный принцип распределения. В каждом процессоре хранится только один блок, размер которого выбирается из соображений равномерности распределения, т.е. NB × N/NPROCS. При этом объекты левой части уравнения распределяются по столбцам, а правой - по строкам. На рисунке 5 представлен пример ленточной матрицы A(7,7)

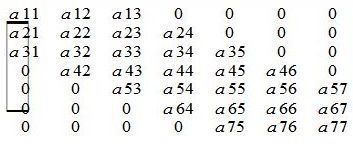
Рис. 5. Пример ленточной матрицы размера 7×7

Для характеристики ленточных матриц вводится параметр ширины ленты BW для симметричных матриц и два параметра BWL (ширина поддиагонали) и BWU (ширина наддиагонали) для несимметричных матриц. Так для рассмотренного на рисунке 5 примера:

• если матрица A симметричная , то BW = 2;
• если матрица A несимметричная, то BWL = 2 и BWU = 2.

Кроме того, если матрица несимметричная, то возможны два варианта факторизации этой матрицы: без выбора главного элемента и с выбором главного элемента столбца. В обоих случаях матрицы хранятся в виде прямоугольных матриц и распределяются по столбцам, однако в первом случае количество строк матрицы равно BWL+BWU+1, во втором 2*(BWL+BWU) +1.

Схема хранения матричных элементов несимметричной матрицы при использовании процедур "без выбора главных элементов" в трех процессорах при условии NB = 3 представлена на рис. 6. Звездочками отмечены неиспользуемые позиции.

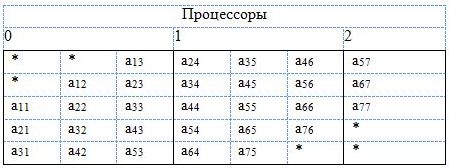
Рис. 6. Распределение по процессорам несимметричной ленточной матрицы для факторизации "без выбора главного элемента"

При использовании процедур "с выбором главного элемента" необходимо предусмотреть выделение дополнительной памяти для рабочих ячеек. Схема распределения матричных элементов в этом случае представлена на рисунке 7, где через F обозначены дополнительные ячейки памяти.

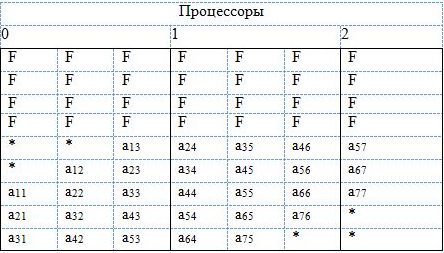
Рис. 7. Распределение по процессорам несимметричной ленточной матрицы для факторизации "с выбором главного элемента"

В случае, когда матрица A является симметричной положительно определенной, достаточно хранить либо нижние поддиагонали (рис. 8), либо верхние (рис. 9).

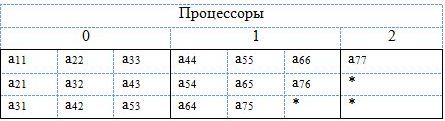
Рис. 8. Распределение по процессорам симметричной положительно определенной ленточной матрицы (UPLO = 'L')

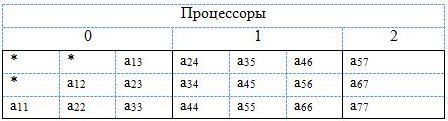
Рис. 9. Распределение по процессорам симметричной положительно определенной ленточной матрицы (UPLO = 'U')

Трехдиагональные матрицы хранятся в виде трех векторов (DU, D, DL) в случае несимметричных матриц (рис. 10) и двух векторов (D, E) для симметричных матриц (рис. 11, 12).

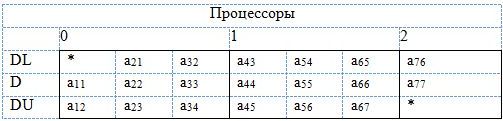
Рис. 10. Пример распределения по процессорам несимметричной трехдиагональной матрицы

Для симметричных матриц в вектор E могут заноситься либо поддиагональные элементы (рис. 11), либо наддиагональные (рис. 12).

Рис. 11. Пример распределения по процессорам симметричной трехдиагональной матрицы (UPLO = 'L')

Рис. 12. Пример распределения по процессорам симметричной трехдиагональной матрицы (UPLO = 'U')

Для всех рассмотренных выше матриц в качестве дескриптора используется массив целого типа из 7 элементов. Его заполнение выполняется напрямую с помощью операторов присваивания, в соответствии со следующей таблицей 3:

Табл. 3. Дескриптор для ленточных и трехдиагональных матриц

 

DESC(1)	= 501	- тип дескриптора;
DESC(2)	= ICTXT	- контекст ансамбля процессоров;
DESC(3)	= N	- число столбцов исходной матрицы;
DESC(4)	= NB	- размер блока по столбцам;
DESC(5)	= ICSRC	- номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0);
DESC(6)	= NROW	- число строк в локальной матрице (leading dimension): NROW= BWL + BWU + 1 для несимметричных матриц в процедурах "без выбора главного элемента"; NROW= 2*(BWL + BWU) + 1 для несимметричных матриц в процедурах" с выбором главного элемента"; NROW= BW + 1 для симметричных положительно определенных матриц; NROW= не используется для трехдиагональных матриц;
DESC(7)		- не используется.

 

Дескриптор для правых частей (таблица 4) имеет такую же структуру, как и для левых. Отличие состоит в том, что разложение по процессорам производится не по столбцам, а по строкам. Кроме того, во избежание лишних пересылок данных, его параметры должны соответствовать параметрам дескриптора для левых частей.

Табл. 4. Дескриптор для правых частей уравнений с ленточными и трехдиагональными матрицами

DESC(1)	= 502	- тип дескриптора;
DESC(2)	= ICTXT	- контекст ансамбля процессоров;
DESC(3)	= M	- число строк исходной матрицы (M = N);
DESC(4)	= MB	- размер блока по строкам (MB = NB);
DESC(5)	= IRSRC	- номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0);
DESC(6)	=NROW	- число строк в локальной матрице (leading dimension) (NROW = NB);
DESC(7)		- не используется.

 

Обращения к подпрограммам библиотеки ScaLAPACK

Обращение к подпрограммам ScaLAPACK рассмотрим на примере вызова подпрограммы решения систем линейных алгебраических уравнений с матрицами общего вида. Имя подпрограммы PDGESV указывает, что:

• тип матриц - double precision (второй символ D);
• матрица общего вида, т.е. не имеет ни симметрии, ни других специальных свойств (3-й и 4-й символы GE);
• подпрограмма выполняет решение системы линейных алгебраических уравнений A * X = B (последние символы SV).

Обращение к подпрограмме имеет вид:

CALL PDGESV (N, NRHS, A, IA, JA, DESCA, IPIV, B, IB, JB, DESCB, INFO)

Здесь

N - размерность исходной матрицы A (полной);

NRHS - количество правых частей в системе (сколько столбцов в матрице B);

А - на входе локальная часть распределенной матрицы A, на выходе локальная часть LU разложения;

IA, JA - индексы левого верхнего элемента подматрицы матрицы A, для которой находится решение (т.е. подразумевается возможность решать систему не для полной матрицы, а для ее части);

DESCA - дескриптор матрицы A (подробно рассмотрен выше);

IPIV - рабочий массив целого типа, который на выходе содержит информацию о перестановках в процессе факторизации. Длина массива должна быть не меньше количества строк в локальной подматрице;

B - на входе - локальная часть распределенной матрицы B, на выходе -локальная часть полученного решения (если решение найдено);

IB, JB - то же самое, что IA, JA для матрицы A;

DESCB - дескриптор матрицы B;

INFO - целая переменная, которая на выходе содержит информацию о том, успешно или нет завершилась подпрограмма, и причину аварийного завершения.

Примерно такой же набор параметров используется для всех драйверных и вычислительных подпрограмм. Назначение их достаточно понятно, следует только внимательно следить за тем, какие параметры относятся к исходным (глобальным) объектам, а какие имеют локальный характер (в первую очередь это касается размерностей массивов и векторов). Подробную информацию обо всех подпрограммах ScaLAPACK можно найти на WWW сервере [27].

Освобождение сетки процессоров

Программы, использующие пакет ScaLAPACK, должны заканчиваться закрытием всех BLACS-процессов. Это осуществляется с помощью вызова подпрограмм:

CALL BLACS_GRIDEXIT (ICTXT) - закрытие контекста;

CALL BLACS_EXIT ( 0 ) - закрытие всех BLACS-процессов.

Примечание: Кроме перечисленных подпрограмм в библиотеку BLACS входят подпрограммы пересылки данных, синхронизации процессов, выполнения глобальных операций по всему ансамблю процессоров или его части (строке или столбцу). Это позволяет обойтись без использования каких-либо других коммуникационных библиотек, тем не менее, допускается и совместное использование BLACS с другими коммуникационными библиотеками. Описание подпрограмм библиотеки BLACS можно найти на сайте netlib.org.

Как отмечалась ранее, библиотека ScaLAPACK, вместе со всеми необходимыми компонентами, входит в распространяемый компанией Intel пакет MKL, который прилагается к дистрибутивам компиляторов. Кроме того, имеется бесплатно распространяемая версия, представленная в виде фортрановских текстов подпрограмм, которые можно откомпилировать и собрать самостоятельно. При этом нужно иметь в виду, что коммуникационная библиотека BLACS тесно привязывается как к архитектуре вычислительной системы, так и к реализации коммуникационной библиотеки MPI. Например, в состав MKL, входят библиотеки BLACS для нескольких реализаций MPI (MVAPICH, IntelMPI, OpenMPI) и при компиляции программ, использующих библиотеку ScaLAPACK, нужно тщательно следить за тем, какая версия MPI является рабочей. В заключение приведем пример простого Makefile'a, с помощью которого можно скомпилировать программу на языке Фортран, использующую библиотеку ScaLAPACK. Подразумевается, что используются библиотеки из пакета Intel MKL. Следует отметить, что библиотека ScaLAPACK ориентирована на язык Фортран с расположением в памяти двумерных массивов по столбцам, поэтому, примеры, приведенные ниже, написаны на Фортране.